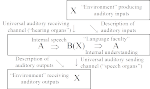When proposing some unorthodox theory, like the modern labor theory of property, orthodox economists always say: “Show me the math!” Well, here it is.
Does Classical Liberalism Imply Democracy?
December 9, 2015 by
This paper, written for a classical liberal audience, goes into the fault line running down the middle of the doctrine: does classical liberalism imply democracy? The libertarian wing, represented concretely today in the startup or charter cities initiatives, only requires consent (and exit) so the consent could be to a non-democratic pact of subjection. The democratic form of classical liberalism is represented by the mature James M. Buchanan who held that a liberal social order required people to be principals in their organizations who could only delegate but not alienate their rights of self-governance. That distinction is traced back to the Reformation inalienability of conscience that descends through the Enlightenment to modern times in the abolitionist and democratic movements.
PBS Making Sen$e blog: The case for employee-owned companies
November 26, 2015 by
This is the “justice in production” argument in a nutshell posted on the PBS Making Sen$e website.
The Existence-Information Duality
October 30, 2015 by
The development of the logic of partitions (dual to the usual Boolean logic of subsets) and logical information theory bring out a fundamental duality between existence (e.g., elements of a subset) and information (e.g., distinctions of a partition). This leads in a more meta-physical vein to two different conceptions of reality, one of which provides the realistic interpretation of quantum mechanics.
Partition Logic talk slides Ljubljana
September 23, 2015 by
Slides from talk on Partition Logic at University of Ljubljana Sept. 8, 2015.
On the Objective Indefiniteness Interpretation of Quantum Mechanics
August 28, 2015 by
Classical physics and quantum physics suggest two different meta-physical conceptions of reality: the classical notion of a objectively definite reality “all the way down,” and the quantum conception of an objectively indefinite type of reality. Part of the problem of interpreting quantum mechanics (QM) is the problem of making sense out of an objectively indefinite reality. Our sense-making strategy is to follow the math by showing that the mathematical way to describe indefiniteness is by partitions (quotient sets or equivalence relations).
1991 clippings on work in Slovenia
July 16, 2015 by
Here are a few newspaper and magazine clippings from my efforts in Slovenia in 1990-91 to get a worker-ownership privatization law drafted and passed.
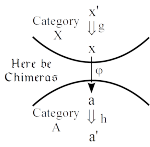
Mac Lane, Bourbaki, and Adjoints Redux
June 16, 2015 by
Saunders Mac Lane famously said that Bourbaki (in the person of Pierre Samuel) “just missed” developing the notion of an adjunction in 1948 a decade before Daniel Kan. When adjoints are defined using heteromorphisms or chimera morphisms (first done by Bodo Pareigis in 1970), then indeed Samuel was only a now-simple dualization away from defining adjoints. Since the heteromorphic treatment allows adjunctions to be factored into two, in general, independent universal mapping properties (UMPs), we also pose the question as to whether adjunctions or UMPs should be considered as category theory’s most important concept. It seems Mac Lane and most orthodox category theorists would say adjunctions but Grothendieck among others would say UMPs stated using representable functors.
On Adjoint and Brain Functors
June 16, 2015 by
We give a heterodox treatment of adjoints using heteromorphisms (object-to-object morphisms between objects of different categories) that parses an adjunction into two separate parts (left and right representations of heteromorphisms). Then these separate parts can be recombined in a new way to define a cognate concept, the brain functor, to abstractly model the functions of perception and action of a brain. This is a preprint of the paper coming out in Axiomathes.
Classical Liberalism and the Firm
March 24, 2015 by
This is a scan of my chapter in the new book: Commerce and Community: Ecologies of Social Cooperation, edited by Robert F. Garnett, Paul Lewis, and Lenore T. Ealy. London: Routledge, 2015.