Semiadjunctions (essentially a formulation of a universal mapping property using hets) turn out to be the appropriate concept for applications of category theory in the life sciences.
Making Enterprises and Markets Responsible
This is a paper written to further Richard Cornuelle’s abiding vision of a more responsible economy and posted here to invite comment. The basic idea is revisit the whole idea of a market economy dominated by absentee-owned and publicly traded corporations (“Wall Street Capitalism”) that disconnect companies (“the Mother of all disconnects”) from the natural desires of the people working in the companies to improve their communities.
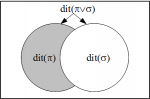
Information as distinctions
This paper is sub-titled “New Foundations for Information Theory” since it is based on the logical notion of entropy from the logic of partitions. The basic logical idea is that of “distinctions.” Logical entropy is normalized counting measure of the set of distinctions of a partition, and Shannon entropy is the number of binary partitions needed, on average, to make the same distinctions of the partition.
Kantian Personhood Principle
This paper formulates the labor theory of property and democratic theory in the context of the Kantian personhood principle to treat other persons always as ends in themselves and never simply as means.
Property and Contract in Economics: The Case for Economic Democracy
This book presents a modern version of the old Labor (or Natural Rights) Theory of Property and of an Inalienable Rights Theory that descends from the Reformation and Enlightenment. Together these theories re-solve the basic problem of distribution in the sense of giving a basis for the just appropriation of property and a basis for answering the question of who is to be the firm, e.g., the suppliers of share capital as in conventional capital, the government as in socialism, or the people who work in the firm as in the system of economic democracy (or labor-managed market economies).
Revisiting Hirschman
This paper revisits the seminal early work of the late Albert Hirschman on development strategy and his critique of the “big push” strategies in order to elucidate the current debates about conditionality-based aid and comprehensive development programs.
Numeraire Illusion: The Final Demise of the Kaldor-Hicks Principle
The result in this paper undercuts the major applications of the Kaldor-Hicks reasoning in the standard Chicago school (wealth maximization) of law and economics, cost–benefit analysis, policy analysis, and related parts of applied welfare economics.