From the 1970’s, there has been almost a half-century of development of employee-owned firms. There has been a wide variety of legal/capital structures that have been tried but too little analysis of which legal forms work or don’t work over the longer term, e.g., the transition from one generation to the next generation of employee-owners. This paper provides a critical analysis of the major forms. The emphasis is the lack of learning between the different forms. The same problems keep recurring even though solutions are known.
Intrinsic versus Extrinsic Motivation
October 6, 2024 by
This paper reviews some of the classic authors and literature on the subtleties of intrinsic motivation in the human activities where a presumed ‘helper’ (teacher, manager, social worker, etc.) are working with a certain class of ‘doers’ (students, workers, clients, etc.).
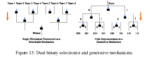
A Fundamental Duality in the Mathematical and Natural Sciences
September 8, 2024 by
This is an essay in what might be called “mathematical metaphysics.” There is a fundamental duality that runs through mathematics and the natural sciences, from logic to biology.
Is “Capitalism” a Misnomer? On Marx’s “capitalism” and Knight’s “civilization”
June 11, 2024 by
This is an open access article from the European Journal of the History of Economic Thought.
The name “capitalism” derives from Marx’s false analogy between medieval land ownership and the “ownership of the means of production.” However, unlike medieval land, capital goods can be rented out, e.g., by Frank Knight’s entrepreneur, and then the capital owner does not hold those management or product rights. What then is the characteristic institution in our civilization? It is the voluntary renting of workers. What then is the relationship between Classical Liberalism, the dominant philosophy behind Economics, and a lifetime labor contract? Frank Knight had plenty to say against the doctrine of inalienable rights which disallows such contracts.
Keiretsu, Proportional Representation, and Input-Output Theory
June 1, 2024 by
This is Chapter 9 in my book: Ellerman, David. 1995. Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics. Lanham MD: Rowman & Littlefield.
This essay grew out of an attempt to model mathematically the possible cross-ownership arrangements that might arise between privatizing firms in the former Yugoslavia [see Ellerman 1991]. The cross-ownership arrangements resemble the groups of Japanese companies called keiretsu. There is cross ownership between the companies in the group as well as some ownership outside the group that is traded on the stock market. In spite of the partial outside ownership, the keiretsu often behave as “self-owning” groups. If firm A owns shares in B, then the management in A usually signs over its proxy on shares in B to the management in firm B. And the management in B does likewise with respect to the managers in A. Thus within certain constraints, each firm can act like a “self-owning” firm, not totally unlike the self-managing firms of the former Yugoslavia.
Parallel Addition, Series-Parallel Duality, and Financial Mathematics
June 1, 2024 by
This is Chapter 12 in my book: Ellerman, David. 1995. Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics. Lanham MD: Rowman & Littlefield.
Valuation rings: A better algebraic treatment of Boolean algebras
June 1, 2024 by
This is Chapter 11 in my book: Ellerman, David. 1995. Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics. Lanham MD: Rowman & Littlefield.
Finding the Markets in the Math: Arbitrage and Optimization Theory
June 1, 2024 by
This is Chapter 10 from my book: Ellerman, David. 1995. Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics. Lanham MD: Rowman & Littlefield.
One of the fundamental insights of mainstream neoclassical economics is the connection between competitive market prices and the Lagrange multipliers of optimization theory in mathematics. Yet this insight has not been well developed. In the standard theory of markets, competitive prices result from the equilibrium of supply and demand schedules. But in a constrained optimization problem, there seems to be no mathematical version of supply and demand functions so that the Lagrange multipliers would be seen as equilibrium prices. How can one “find the markets in the math” so that Lagrange multipliers will emerge as equilibrium market prices?
Category Theory as the Theory of Concrete Universals
June 1, 2024 by
This is Chapter 8 of my book: Ellerman, David. 1995. Intellectual Trespassing as a Way of Life: Essays in Philosophy, Economics, and Mathematics. Lanham MD: Rowman & Littlefield.
This essay deals with a connection between a relatively recent (1940s and 1950s) field of mathematics, category theory, and a hitherto vague notion of philosophical logic usually associated with Plato, the self-predicative universal or concrete universal. Consider the following example of “bad Platonic metaphysics.”
Given all the entities that have a certain property, there is one entity among them that exemplifies the property in an absolutely perfect and universal way. It is called the “concrete universal.” There is a relationship of “participation” or “resemblance” so that all the other entities that have the property “participate in” or “resemble” that perfect example, the concrete universal.
All of this and much more “bad metaphysics” turns out to be precisely modeled in category theory.