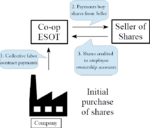
This paper shows how a worker cooperative can serve as an ESOP-like employee-ownership vehicle to make a partial or total buyout of a conventional company.
Source-paper on theory of inalienability
This paper is only a collection of likenesses and representative quotations from thinkers about inalienability and inalienable rights starting from Antiquity down to the present.
Some Less Well-Known Supporters of Workplace Democracy
This is a collection of likenesses or pictures and some representative quotations of a number of less well-known supporters (all dead white men) of workplace democracy.
Alleged Problems in Labor-Managed Firms
This paper will discuss two problems that have plagued the literature on the Ward-Domar-Vanek labor-managed firm (LMF) model, the perverse supply response problem and the Furubotn-Pejovich horizon problem.
Lord Eustace Percy’s “Unknown State” Lecture
Lord Eustace Percy was a Conservative public servant but was better known as a serious thinker, indeed, as the “Minister of Thinking.” There is a remarkable and much-quoted passage in his 1944 Riddell Lecture The Unknown State.
A Note on Spencer-Brown’s Algebra
George Spencer-Brown in his cryptic book, Laws of Form, started off reasoning about “the Distinction” and ended up with an algebra that later writers showed to be the Boolean algebra of two elements.
Panopticon vs. McGregor’s Theory Y
This paper is part of a larger project to better understand the limitations of the economic theory of agency and incentives. The economic approach focuses on extrinsic incentives whereas a better understanding of human organization requires an understanding of intrinsic motivation and the complementary or substitutive relationships with extrinsic motivation.
English and Swedish Versions of Swedish ESOP Report
In September 2017, my long-time associate, Chris Mackin, and I did a speaking tour on ESOPs in Sweden hosted by the filmmaker, Patrik Witkowsky, the to-be-lawyer, Mattias Göthberg, and the labor-oriented think tank, Katalyst. Afterwards, Patrik wrote a report, here translated into English, introducing the ESOP idea to a larger Swedish audience and describing the US experience.
Talk: Hamming distance in classical and quantum logical information theory
This is a set of slides from a talk on introducing the Hamming distance into classical logical information theory and then developing the quantum logical notion of Hamming distance–which turns out to equal a standard notion of distance in quantum information theory, the Hilbert-Schmidt distance.
New Work for the Visible Hand of Business
This is an essay about the late Richard Cornuelle’s essay “New work for invisible hands” in a commemorative volume of Conversations on Philanthropy.