This paper gives a toy model of quantum mechanics over the field 2, where the vectors can be interpreted as subsets of a universe set, and hence the name: “Quantum mechanics over sets.” It gives the “logic” of QM in the old-fashioned sense of the essential logic of a theory pared down to operations on sets (vectors over 2). This includes the simplest logical treatment of the double-slit experiment, Bell’s Theorem, the probability calculus based on Born’s Rule, and much else (all restated in the context of sets).
Determination through universals
May 28, 2013 by
Semiadjunctions (essentially a formulation of a universal mapping property using hets) turn out to be the appropriate concept for applications of category theory in the life sciences.
Information as distinctions
January 23, 2013 by
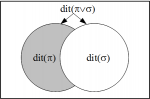
This paper is sub-titled “New Foundations for Information Theory” since it is based on the logical notion of entropy from the logic of partitions. The basic logical idea is that of “distinctions.” Logical entropy is normalized counting measure of the set of distinctions of a partition, and Shannon entropy is the number of binary partitions needed, on average, to make the same distinctions of the partition.
The Logic of Partitions: Introduction to the Dual of the Logic of Subsets
December 11, 2012 by
Partitions on a set are dual to subsets of a set in the sense of the category-theoretic duality of epimorphisms and monomorphisms. Modern categorical logic as well as the Kripke models of intuitionistic logic suggest that the interpretation of classical “propositional” logic should be the logic of subsets of a given universe set. The propositional interpretation is isomorphic to the special case where the truth and falsity of propositions behave like the subsets of a one-element set. If classical “propositional” logic is thus seen as the logic of subsets of a universe set, then the question naturally arises of a dual logic of partitions on a universe set. This paper is an introduction to that logic of partitions dual to classical “propositional” logic.
Counting Distinctions
December 11, 2012 by
This paper gives the logical theory of information that is developed out of partition logic in exactly the same way that Boole developed logical probability theory out of his subset logic.
Adjoints and Emergence
December 11, 2012 by
Given the importance of adjoint funtors in mathematics, it seems appropriate to look for empirical applications. The focus here is on applications in the life sciences (e.g., selectionist mechanisms) and human sciences (e.g., the generative grammar view of language).
Adjoints and Brain Functors
December 11, 2012 by
These slides define the potentially important notion of a brain functor which is a cognate of the notion of adjoint functors.
Adjoint Functors and Heteromorphisms
December 11, 2012 by
This heteromorphic theory of adjoint functors shows that all adjunctions arise from the birepresentations of the heteromorphisms between the objects of different categories.
A Theory of Adjoint Functors
December 11, 2012 by
Our focus in this paper is to present a theory of adjoint functors, a theory which shows that all adjunctions arise from the birepresentations of “chimera” morphisms or “heteromorphisms” between objects in different categories.
Category Theory and Concrete Universals
December 11, 2012 by
This old paper, published in Erkenntnis, deals with a connection between a relatively recent (1940s and 1950s) field of mathematics, category theory, and a hitherto vague notion of philosophical logic usually associated with Plato, the self-predicative universal or concrete universal.