Category theory has foundational importance because it provides conceptual lenses to characterize what is important and universal in mathematics—with adjunctions being the primary lense. If adjunctions are so important in mathematics, then perhaps they will isolate concepts of some importance in the empirical sciences. But the applications of adjunctions have been hampered by an overly restrictive formulation that avoids heteromorphisms or hets. By reformulating an adjunction using hets, it is split into two parts, a left and a right semiadjunction (or half-adjunuction). Semiadjunctions (essentially a formulation of a universal mapping property using hets) turn out to be the appropriate concept for applications in the life sciences. The semiadjunctions characterize three principal schemes with applications:
1. determination through a receiving universal (e.g., natural selection, perception, language acquisition, recursion, and language understanding);
2. determination through a sending universal (e.g., intentional action, DNA mechanism to build amino acids, hierarchy of regulatory genes to build organs, stem cells, and language production), and
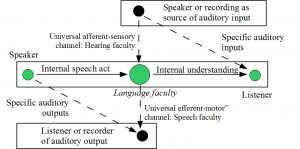
3. two-way determination with one universal as both receiving and sending (e.g., perception/action and language understanding/production).
Determination through universals
May 28, 2013 by