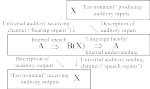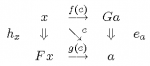Semiadjunctions (essentially a formulation of universal mapping properties using hets) can be recombined in a new way to define the notion of a brain functor that provides an abstract model of the intentionality of perception and action (as opposed to the passive reception of sense-data or the reflex generation of behavior).
The Joy of Hets (talk slides)
February 29, 2016 by
These are the slides from a talk on the role of heteromorphisms (hets) in category theory given at the Category Theory Seminar at NYU on January 13, 2016.
Mac Lane, Bourbaki, and Adjoints Redux
June 16, 2015 by
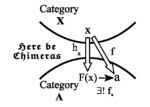
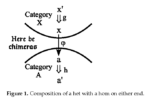
Saunders Mac Lane famously said that Bourbaki (in the person of Pierre Samuel) “just missed” developing the notion of an adjunction in 1948 a decade before Daniel Kan. When adjoints are defined using heteromorphisms or chimera morphisms (first done by Bodo Pareigis in 1970), then indeed Samuel was only a now-simple dualization away from defining adjoints. Since the heteromorphic treatment allows adjunctions to be factored into two, in general, independent universal mapping properties (UMPs), we also pose the question as to whether adjunctions or UMPs should be considered as category theory’s most important concept. It seems Mac Lane and most orthodox category theorists would say adjunctions but Grothendieck among others would say UMPs stated using representable functors.
On Adjoint and Brain Functors
June 16, 2015 by
We give a heterodox treatment of adjoints using heteromorphisms (object-to-object morphisms between objects of different categories) that parses an adjunction into two separate parts (left and right representations of heteromorphisms). Then these separate parts can be recombined in a new way to define a cognate concept, the brain functor, to abstractly model the functions of perception and action of a brain. This is a preprint of the paper coming out in Axiomathes.
Determination through universals
May 28, 2013 by
Semiadjunctions (essentially a formulation of a universal mapping property using hets) turn out to be the appropriate concept for applications of category theory in the life sciences.
Adjoints and Emergence
December 11, 2012 by
Given the importance of adjoint funtors in mathematics, it seems appropriate to look for empirical applications. The focus here is on applications in the life sciences (e.g., selectionist mechanisms) and human sciences (e.g., the generative grammar view of language).
Adjoints and Brain Functors
December 11, 2012 by
These slides define the potentially important notion of a brain functor which is a cognate of the notion of adjoint functors.
Adjoint Functors and Heteromorphisms
December 11, 2012 by
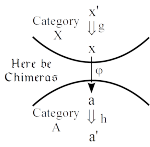
This heteromorphic theory of adjoint functors shows that all adjunctions arise from the birepresentations of the heteromorphisms between the objects of different categories.
A Theory of Adjoint Functors
December 11, 2012 by
Our focus in this paper is to present a theory of adjoint functors, a theory which shows that all adjunctions arise from the birepresentations of “chimera” morphisms or “heteromorphisms” between objects in different categories.