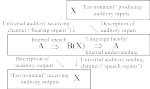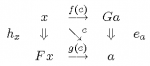Classical physics and quantum physics suggest two different meta-physical conceptions of reality: the classical notion of a objectively definite reality “all the way down,” and the quantum conception of an objectively indefinite type of reality. Part of the problem of interpreting quantum mechanics (QM) is the problem of making sense out of an objectively indefinite reality. Our sense-making strategy is to follow the math by showing that the mathematical way to describe indefiniteness is by partitions (quotient sets or equivalence relations).
Mac Lane, Bourbaki, and Adjoints Redux
June 16, 2015 by
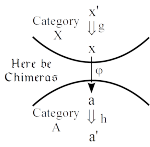
Saunders Mac Lane famously said that Bourbaki (in the person of Pierre Samuel) “just missed” developing the notion of an adjunction in 1948 a decade before Daniel Kan. When adjoints are defined using heteromorphisms or chimera morphisms (first done by Bodo Pareigis in 1970), then indeed Samuel was only a now-simple dualization away from defining adjoints. Since the heteromorphic treatment allows adjunctions to be factored into two, in general, independent universal mapping properties (UMPs), we also pose the question as to whether adjunctions or UMPs should be considered as category theory’s most important concept. It seems Mac Lane and most orthodox category theorists would say adjunctions but Grothendieck among others would say UMPs stated using representable functors.
On Adjoint and Brain Functors
June 16, 2015 by
We give a heterodox treatment of adjoints using heteromorphisms (object-to-object morphisms between objects of different categories) that parses an adjunction into two separate parts (left and right representations of heteromorphisms). Then these separate parts can be recombined in a new way to define a cognate concept, the brain functor, to abstractly model the functions of perception and action of a brain. This is a preprint of the paper coming out in Axiomathes.
Partitions and Objective Indefiniteness in Quantum Mechanics
January 9, 2014 by
The problem of interpreting quantum mechanics (QM) is essentially the problem of making sense out of an objectively indefinite reality–that is described mathematically by partitions. Our sense-making strategy is implemented by developing the mathematics of partitions at the connected conceptual levels of sets and vector spaces. Set concepts are transported to (complex) vector spaces to yield the mathematical machinery of full QM, and the complex vector space concepts of full QM are transported to the set-like vector spaces over ℤ₂ to yield the rather fulsome pedagogical model of quantum mechanics over sets or QM/sets.
Adjoints and Emergence
December 11, 2012 by
Given the importance of adjoint funtors in mathematics, it seems appropriate to look for empirical applications. The focus here is on applications in the life sciences (e.g., selectionist mechanisms) and human sciences (e.g., the generative grammar view of language).
Adjoints and Brain Functors
December 11, 2012 by
These slides define the potentially important notion of a brain functor which is a cognate of the notion of adjoint functors.
Adjoint Functors and Heteromorphisms
December 11, 2012 by
This heteromorphic theory of adjoint functors shows that all adjunctions arise from the birepresentations of the heteromorphisms between the objects of different categories.
A Theory of Adjoint Functors
December 11, 2012 by
Our focus in this paper is to present a theory of adjoint functors, a theory which shows that all adjunctions arise from the birepresentations of “chimera” morphisms or “heteromorphisms” between objects in different categories.
Category Theory and Concrete Universals
December 11, 2012 by
This old paper, published in Erkenntnis, deals with a connection between a relatively recent (1940s and 1950s) field of mathematics, category theory, and a hitherto vague notion of philosophical logic usually associated with Plato, the self-predicative universal or concrete universal.
Concrete Universals in Category Theory
December 11, 2012 by
This old essay deals with a connection between a relatively recent (1940s and 1950s) field of mathematics, category theory, and a hitherto vague notion of philosophical logic usually associated with Plato, the self-predicative universal or concrete universal.